O Blog está em fase de formação então , dúvidas , dicas e qualquer coisa relacionada ao tema .. Só comentar , pedir conteúdo e tudo mais !
Obrigado.
sexta-feira, 26 de outubro de 2012
Funçoes trigonométricas
Função seno
Chamamos de função seno a função f(x) = sen x
O domínio dessa função é R e a imagem é Im [ -1,1] ; visto que, na circunferência trigonométrica o raio é unitário e, pela definição do seno, –1 £ sen x £ 1, ou seja:
Domínio de f(x) = sen x; D(sen x) = R.
Imagem de f(x) = sen x; Im(sen x) = [ -1,1] .
Sinal da Função: Como seno x é a ordenada do ponto-extremidade do arco:1
f(x) = sen x é positiva no 1° e 2° quadrantes (ordenada positiva)
f(x) = sen x é negativa no 3° e 4° quadrantes (ordenada negativa)

Observe que esse gráfico é razoável, Pois:
Quando  , 1º quadrante, o valor de sen x cresce de 0 a 1.
, 1º quadrante, o valor de sen x cresce de 0 a 1.
Quando  , 2º quadrante, o valor de sen x decresce de 1 a 0.
, 2º quadrante, o valor de sen x decresce de 1 a 0.
Quando  , 3º quadrante, o valor de sen x decresce de 0 a -1.
, 3º quadrante, o valor de sen x decresce de 0 a -1.
Quando  , 4º quadrante, o valor de sen x cresce de -1 a 0.]
, 4º quadrante, o valor de sen x cresce de -1 a 0.]
Função cosseno
O domínio dessa função é
R e a imagem é Im [ -1,1] ; visto que, na circunferência
trigonométrica o raio é unitário e, pela definição do cosseno, –1 £ cos x
£ 1, ou seja:
Domínio de f(x) = cos x; D(cos x) = R.
Imagem de f(x) = cos x; Im(cos x) = [ -1,1] .
Sinal da Função: Como cosseno x é a abscissa do ponto-extremidade do arco:
f(x) = cos x é positiva no 1° e 2° quadrantes (abscissa positiva)
f(x) = cos x é negativa no 3° e 4° quadrantes (abscissa negativa)

Observe que esse gráfico é razoável, Pois:
Quando  , 1º quadrante, o valor do cos x decresce de 1 a 0.
, 1º quadrante, o valor do cos x decresce de 1 a 0.
Quando  , 2º quadrante, o valor do cos x decresce de 0 a -1.
, 2º quadrante, o valor do cos x decresce de 0 a -1.
Quando  , 3º quadrante, o valor do cos x cresce de -1 a 0.
, 3º quadrante, o valor do cos x cresce de -1 a 0.
Quando ,  4º quadrante, o valor do cos x cresce de 0 a 1.
4º quadrante, o valor do cos x cresce de 0 a 1.
Função tangente
Chamamos de função tangente a função f(x) = tg x.
Domínio de f(x) = O domínio dessa função são todos os números reais, exceto os que zeram o cosseno pois não existe cosx = 0
Imagem de f(x) = tg x; Im(tg x) = R ou
Sinal da Função: Como tangente x é a ordenada do ponto T interseção da reta que passa pelo centro de uma circunferência trigonométrica e o ponto-extremidade do arco, com o eixo das tangentes então:
f(x) = tg x é positiva no 1° e 3° quadrantes (produto da ordenada pela abscissa positiva)
f(x) = tg x é negativa no 2° e 4° quadrantes (produto da ordenada pela abscissa negativa)
quarta-feira, 24 de outubro de 2012
Seus Problemas Acabaram,,,
Estou trazendo pra vocês hoje , um MEGA RESUMÃO de TODAS AS FORMULAS DE MATEMÁTICA ..
Pra muitos uma salvação !
TODAS AS FORMULAS MATEMATICAS
Pra muitos uma salvação !
TODAS AS FORMULAS MATEMATICAS
Trigonometria de Meia Volta .
''O seno de um angulo é igual o cosseno do seu complemento ( Angulo que somado dê resultado 90 )''
Exemplo :
Seno de 30° é igual ao Cosseno de 60°
Seno de 37° é igual ao Cosseno de 53 °
E assim sucessivamente ...
Relaçoes trigonométricas num triangulo qualquer - Seno e cosseno de angulos suplementares ( Ângulos que somados dê resultado 180° )
Seno de um ângulo obtuso (180° > A > 90° ) é igual ao seno do ângulo agudo suplementar .
Sen A = Sen ( 180° - A )
Cosseno de um ângulo obtuso é igual ao OPOSTO do cosseno do angulo agudo suplementar
Cos A = - Cos (180 - A )
Lei dos Senos .


Na lei dos senos utilizamos relações envolvendo o seno do ângulo e a medida oposta ao ângulo.
Exemplo 1
Determine o valor de x no triângulo a seguir.
Exemplo 1
Determine o valor de x no triângulo a seguir.

sen120º = sen(180º – 120º) = sen60º = √3/2 ou 0,865
sen45º = √2/2 ou 0,705

sen45º = √2/2 ou 0,705

Exemplo 2
No triângulo a seguir temos dois ângulos, um medindo 45º, outro medindo 105º, e um dos lados medindo 90 metros. Com base nesses valores determine a medida de x.
No triângulo a seguir temos dois ângulos, um medindo 45º, outro medindo 105º, e um dos lados medindo 90 metros. Com base nesses valores determine a medida de x.

Para determinarmos a medida de x no triângulo devemos utilizar a lei
dos senos, mas para isso precisamos descobrir o valor do terceiro ângulo
do triângulo. Para tal cálculo utilizamos a seguinte definição: a soma
dos ângulos internos de um triângulo é igual a 180º. Portanto:
α + 105º + 45º = 180º
α + 150º = 180º
α = 180º – 150º
α = 30º
Aplicando a lei dos senos

Por Marcos Noé - Graduado em Matemática.
α + 105º + 45º = 180º
α + 150º = 180º
α = 180º – 150º
α = 30º
Aplicando a lei dos senos

Por Marcos Noé - Graduado em Matemática.
Lei dos Cossenos
Utilizamos a lei dos cossenos nas situações envolvendo triângulos não
retângulos, isto é, triângulos quaisquer. Esses triângulos não possuem
ângulo reto, portanto as relações trigonométricas do seno, cosseno e
tangente não são válidas. Para determinarmos valores de medidas de
ângulos e medidas de lados utilizamos a lei dos cossenos, que é expressa
pela seguinte lei de formação:


Exemplo 1
Utilizando a lei dos cossenos, determine o valor do segmento x no triângulo a seguir:
Utilizando a lei dos cossenos, determine o valor do segmento x no triângulo a seguir:

a² = b² + c² – 2 * b * c * cos?
7² = x² + 3² – 2 * 3 * x * cos60º
49 = x² + 9 – 6 * x * 0,5
49 = x² + 9 – 3x
x² –3x – 40 = 0
Aplicando o método resolutivo da equação do 2º grau, temos:
x’ = 8 e x” = – 5, por se tratar de medidas descartamos x” = –5 e utilizamos x’ = 8. Então o valor de x no triângulo é 8 cm.
Exemplo 2
Em um triângulo ABC, temos as seguintes medidas: AB = 6 cm, AC = 5 cm e BC = 7 cm. Determine a medida do ângulo A.
Vamos construir o triângulo com as medidas fornecidas no exercício.
7² = x² + 3² – 2 * 3 * x * cos60º
49 = x² + 9 – 6 * x * 0,5
49 = x² + 9 – 3x
x² –3x – 40 = 0
Aplicando o método resolutivo da equação do 2º grau, temos:
x’ = 8 e x” = – 5, por se tratar de medidas descartamos x” = –5 e utilizamos x’ = 8. Então o valor de x no triângulo é 8 cm.
Exemplo 2
Em um triângulo ABC, temos as seguintes medidas: AB = 6 cm, AC = 5 cm e BC = 7 cm. Determine a medida do ângulo A.
Vamos construir o triângulo com as medidas fornecidas no exercício.

Aplicando a lei dos cossenos
a = 7, b = 6 e c = 5
7² = 6² + 5² – 2 * 6 * 5 * cos A
49 = 36 + 25 – 60 * cos A
49 – 36 – 25 = –60 * cos A
–12 = –60 * cos A
12 = 60 * cos A
12/60 = cos A
cos A = 0,2
O ângulo que possui cosseno com valor aproximado de 0,2 mede 78º.
Exemplo 3
Calcule a medida da maior diagonal do paralelogramo da figura a seguir, utilizando a lei dos cossenos.

cos 120º = –cos(180º – 120º) = – cos 60º = – 0,5
x² = 5² + 10² – 2 * 5 * 10 * ( – cos 60º)
x² = 25 + 100 – 100 * (–0,5)
x² = 125 + 50
x² = 175
√x² = √175
x = √5² * 7
x = 5√7
Portanto, a diagonal do paralelogramo mede 5√7 cm.
x² = 5² + 10² – 2 * 5 * 10 * ( – cos 60º)
x² = 25 + 100 – 100 * (–0,5)
x² = 125 + 50
x² = 175
√x² = √175
x = √5² * 7
x = 5√7
Portanto, a diagonal do paralelogramo mede 5√7 cm.
Fonte : Livro : Matemática fundamental , Uma nova aboirdagem ( José Rui Giovanni / José Roberto Bonjorno / José Rui Giovanni Jr. )
http://www.brasilescola.com/matematica/lei-dos-senos.htm
http://www.brasilescola.com/matematica/lei-coseno.htm
Circulo e Circunferência ( Resumão )


Perímetro ou Comprimento da Circunferência: A extensão da circunferência, ou seja, seu perímetro pode ser calculada através da equação: C= π.d ou C=π.2.r, onde:
- C=comprimento
- π (pi)=3,1415...(aproximadamente)
- d=diâmetro
- r=raio
- π (pi) =3,1415... (aproximadamente)
- r=raio
Raio:
Raio de uma circunferência (ou de um círculo) é um segmento de reta com
uma extremidade no centro da circunferência e a outra extremidade num
ponto qualquer da circunferência. O raio é a metade de um diâmetro.
Diâmetro: Diâmetro de uma circunferência (ou de um círculo) é uma corda que passa pelo centro da circunferência. Observamos que o diâmetro é a maior corda da circunferência.
O diâmetro é o dobro do raio.
Diâmetro: Diâmetro de uma circunferência (ou de um círculo) é uma corda que passa pelo centro da circunferência. Observamos que o diâmetro é a maior corda da circunferência.
O diâmetro é o dobro do raio.
Corda: Corda
de uma circunferência é um segmento de reta cujas extremidades
pertencem à circunferência. Segmentos determinados por dois pontos
quaisquer da circunferência são cordas da circunferência. Na figura os
segmentos de reta AB e CD são cordas.

Reta secante: Uma reta
é secante a uma circunferência se ela intercepta a circunferência em
dois pontos quaisquer. Propriedade: É perpendicular ao raio pelo seu
ponto médio.

Reta tangente: Uma
reta é tangente à circunferência se a intercepta em um único ponto.
Propriedade: É perpendicular ao raio em seu ponto de tangência.
 Daí surge a função trigonométrica Tangente !
Daí surge a função trigonométrica Tangente !
Reta externa: uma reta externa é aquela que não intercepta nenhum ponto da circunferência.

Fonte : http://faliolor.blogspot.com.br/2008/08/crculo-e-circunferncia.html
Área de Figuras Planas
Cálculo da Área do Triângulo
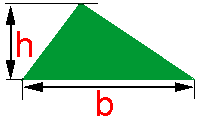 Denominamos de triângulo a um polígono de três lados.
Denominamos de triângulo a um polígono de três lados.Observe a figura ao lado. A letra h representa a medida da altura do triângulo, assim como letra b representa a medida da sua base.
A área do triângulo será metade do produto do valor da medida da base, pelo valor da medida da altura, tal como na fórmula abaixo:
A letra S representa a área ou superfície do triângulo.
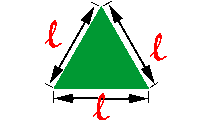 No caso do triângulo equilátero, que possui os três ângulos internos
iguais, assim como os seus três lados, podemos utilizar a seguinte
fórmula:
No caso do triângulo equilátero, que possui os três ângulos internos
iguais, assim como os seus três lados, podemos utilizar a seguinte
fórmula:Onde l representa a medida dos lados do triângulo.
Cálculo da Área do Paralelogramo
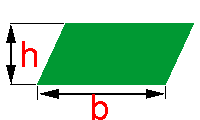 Um quadrilátero cujos lados opostos são iguais e paralelos é denominado paralelogramo.
Um quadrilátero cujos lados opostos são iguais e paralelos é denominado paralelogramo.Com h representando a medida da sua altura e com b representando a medida da sua base, a área do paralelogramo pode ser obtida multiplicando-se b por h, tal como na fórmula abaixo:
Cálculo da Área do Losango
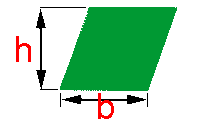 O losango é um tipo particular de paralelogramo. Neste caso além dos lados opostos serem paralelos, todos os quatro lados são iguais.
O losango é um tipo particular de paralelogramo. Neste caso além dos lados opostos serem paralelos, todos os quatro lados são iguais.Se você dispuser do valor das medidas h e b, você poderá utilizar a fórmula do paralelogramo para obter a área do losango.
Outra característica do losango é que as suas diagonais são perpendiculares.
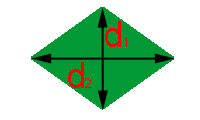 Observe na figura à direita, que a partir das diagonais podemos dividir o losango em quatro triângulos iguais.
Observe na figura à direita, que a partir das diagonais podemos dividir o losango em quatro triângulos iguais.Consideremos a base b como a metade da diagonal d1 e a altura h como a metade da diagonal d2, para calcularmos a área de um destes quatro triângulos. Bastará então que a multipliquemos por 4, para obtermos a área do losango. Vejamos:
Realizando as devidas simplificações chegaremos à fórmula:
Cálculo da Área do Quadrado
Todo quadrado é também um losango, mas nem todo losango vem a ser um quadrado, do mesmo modo que todo quadrado é um retângulo, mas nem todo retângulo é um quadrado.O quadrado é um losango, que além de possuir quatro lados iguais, com diagonais perpendiculares, ainda possui todos os seus ângulos internos iguais a 90°. Observe ainda que além de perpendiculares, as diagonais também são iguais.
Por ser o quadrado um losango e por ser o losango um paralelogramo, podemos utilizar para o cálculo da área do quadrado, as mesmas fórmulas utilizadas para o cálculo da área tanto do losango, quanto do paralelogramo.
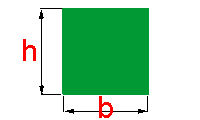 Quando dispomos da medida do lado do quadrado, podemos utilizar a fórmula do paralelogramo:
Quando dispomos da medida do lado do quadrado, podemos utilizar a fórmula do paralelogramo:Como h e b possuem a mesma medida, podemos substituí-las por l, ficando a fórmula então como sendo:
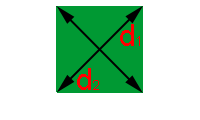 Quando dispomos da medida das diagonais do quadrado, podemos utilizar a fórmula do losango:
Quando dispomos da medida das diagonais do quadrado, podemos utilizar a fórmula do losango:Como ambas as diagonais são idênticas, podemos substituí-las por d, simplificando a fórmula para:
Cálculo da Área do Retângulo
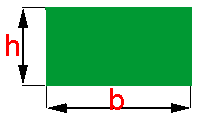 Por definição o retângulo é um quadrilátero equiângulo (todo os seus
ângulos internos são iguais), cujos lados opostos são iguais.
Por definição o retângulo é um quadrilátero equiângulo (todo os seus
ângulos internos são iguais), cujos lados opostos são iguais.Se todos os seus quatro lados forem iguais, teremos um tipo especial de retângulo, chamado de quadrado.
Por ser o retângulo um paralelogramo, o cálculo da sua área é realizado da mesma forma.
Se denominarmos as medidas dos lados de um retângulo como na figura ao lado, teremos a seguinte fórmula:
Cálculo da Área do Círculo
 A divisão do perímetro de uma circunferência, pelo seu diâmetro
resultará sempre no mesmo valor, qualquer que seja circunferência. Este
valor irracional constante é representado pela letra grega minúscula pi, grafada como:
A divisão do perímetro de uma circunferência, pelo seu diâmetro
resultará sempre no mesmo valor, qualquer que seja circunferência. Este
valor irracional constante é representado pela letra grega minúscula pi, grafada como:Por ser um número irracional, o número pi possui infinitas casas decimais. Para cálculos corriqueiros, podemos utilizar o valor 3,14159265. Para cálculos com menos precisão, podemos utilizar 3,1416, ou até mesmo 3,14.
O perímetro de uma circunferência é obtido através da fórmula:
O cálculo da área do círculo é realizado segundo a fórmula abaixo:
Onde r representa o raio do círculo.
Cálculo da Área de Setores Circulares
 O cálculo da área de um setor circular pode ser realizado
calculando-se a área total do círculo e depois se montando uma regra de
três, onde a área total do círculo estará para 360°, assim como a área
do setor estará para o número de graus do setor.
O cálculo da área de um setor circular pode ser realizado
calculando-se a área total do círculo e depois se montando uma regra de
três, onde a área total do círculo estará para 360°, assim como a área
do setor estará para o número de graus do setor.Sendo S a área total do círculo, Sα a área do setor circular e α o seu número de graus, temos:
Em radianos temos:
A partir destas sentenças podemos chegar a esta fórmula em graus:
E a esta outra em radianos:
Onde r representa o raio do círculo referente ao setor e α é o ângulo também referente ao setor.
Cálculo da Área de Coroas Circulares
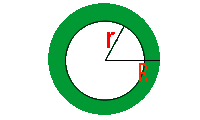 O cálculo da área de uma coroa circular pode ser realizado
calculando-se a área total do círculo e subtraindo-se desta, a área do
círculo inscrito. Podemos também utilizar a seguinte fórmula:
O cálculo da área de uma coroa circular pode ser realizado
calculando-se a área total do círculo e subtraindo-se desta, a área do
círculo inscrito. Podemos também utilizar a seguinte fórmula:Onde R representa o raio do círculo e r representa o raio do círculo inscrito.
Fonte : http://www.matematicadidatica.com.br/GeometriaCalculoAreaFigurasPlanas.aspx
Obrigado.
Assinar:
Comentários (Atom)



